真空から。

今は航空学徒、春から数理情報学徒になるひとの備忘録やメモです。

全ては収束する〜ボルツマン方程式とResNetにみるtrend to equilibrium~

ご無沙汰しております。真空です。今年ももうアドベントカレンダーの時期がやってきました。

昨年の１２月が３ヶ月前に思える今日この頃ですが、みなさんはどうでしょうか？

 

今年は東京大学航空宇宙工学科／専攻 Advent Calendar 2020一日目、ならびに物工/計数 Advent Calendar 2020二日目の二つの記事として書くことになりました。

adventar.org

adventar.org

 

年を食うと所属が変わったり増えたりするものですが、こんな感じでだんだん書くアドベントカレンダーも増えていくんでしょうね。大変です・・・今年も既に大変だったので・・・。

大変だったので今年はmathlogという数式が打ちやすいと話題のやつで記事を書きました。こっちに移植しようとしたのですが失敗したので以下に貼り付けるにとどめます。

 

mathlog.info

 

内容を一言でまとめると

適切に学習された（推定対象から適切にパラメータが定められた）ResNetの層方向への情報伝達は、運動則に基づくBoltzmann方程式のtrend to equilibriumだと理解できる

です。気になったら見てみてください。

ではでは皆さん良い１２月を〜〜

ランキン・ユゴニオってそんなに大事？～圧縮性流体入門から保存則の偏微分方程式論、そして渋滞へ～

おはこんばんにちは。卒論やってたら更新がめっちゃ遅くなってしまいました、ごめんなさい（土下座）。ブログ続けるのってむずかしい・・・

 

今日は東京大学航空宇宙アドベントカレンダー2019一日目ということで、タイトルにもある通り、航空宇宙ゴリゴリ、かつ今の研究にちょっと関連する話（できれば来年の研究にも）の内容を書きたいと思います。

adventar.org

 

（院試勉強関連の話は春休みくらいに再開するつもりなのでしばしお待ちください。）

 

最初に要旨をまとめておくと

  1. 圧縮性流体の一番最初に''定常な''垂直衝撃波（不連続面）前後の物理量を関係づけるRankine-Hugoniotの式を習いますが、なんで名前が付いてる（ほど重要な）のかわからん
  2. 実は、ある特殊なクラスの発展（''非定常''）方程式（保存則：Conservation law）が不連続解を持つ条件のことをランキン・ユゴニオ条件という！
  3. ランキン・ユゴニオ条件の観点から車の渋滞現象をみてみるとちょっと面白い。

という感じです。

そんなわけで今日のお品書きは☟みたいになってます。

では内容に入っていきましょう。

圧縮性流体力学超入門～Rankine-Hugoniot 関係式導出～

まずは航空宇宙らしく、圧縮性流体力学の入門からやりましょう。音速より速い流体の運動、つまり超音速流れでは圧力や密度が不連続変化する現象が見られます。この不連続変化する面を衝撃波といいます。

f:id:nobo0409mathinfo:20191129175706j:plain

シュリーレン法により撮影された衝撃波。wikiより転載。シュリーレン法は院試に出てましたね。

衝撃波の中でも、伝播方向に対して波面（不連続面）が垂直になっているものを垂直衝撃波といいます。垂直じゃないやつは斜め衝撃波です（上図）。単純ですね。斜め衝撃波は式が無駄にめんどいので、以下では次の図にあるような垂直衝撃波を考えます。Pは圧力、 \rhoは密度、uは衝撃波進行方向速度（そうでない方向は今回考えない）、Tは温度、Mはマッハ数です。

 

f:id:nobo0409mathinfo:20191129182303g:plain

垂直衝撃波（SW）前後の物理量。http://www.ipc.tohoku-gakuin.ac.jp/simlab/fegs/prog12d.html から引用。

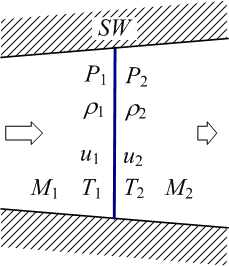
連続（もっと強くいえば微分可能な）な現象であれば運動方程式などの微分方程式をもちいて時間発展を逐一追っていくことによって任意の時刻の物理量を求めることができます。しかし、今回は不連続な面が存在するので、そのような方法はうまくいきません。

こういう状況は高校物理だと物体の二体衝突の問題なんかがありました。そのときはどうしたかというと運動量保存則（と反発係数に関する式）を用いたのでした。今回もそのような保存則を用いる発想で衝撃波前後の物理量の変化、特に圧力比\dfrac{p_2}{p_1}と密度比\dfrac{\rho_2}{\rho_1}の関係式を求めてみましょう。

不連続面は薄いとして、断面積の変化・摩擦・熱の流入出がないと仮定します。この状況で成り立つ保存則は以下の三つです。

  1. 質量保存則\begin{equation} \rho_1u_1= \rho_2u_2\end{equation}
  2. 運動量保存則\begin{equation} p_1+ \rho_1{u_1}^2=p_2+ \rho_2 {u_2}^2 \end{equation}
  3. エネルギー保存則\begin{equation} \frac{\gamma}{\gamma-1}\frac{p_1}{ \rho_1}+\frac{1}{2}u_1^2=\frac{\gamma}{\gamma-1}\frac{p_2}{ \rho_2}+\frac{1}{2}u_2^2 \end{equation}

いきなりこの式書かれても、、、と思う方もいると思うので軽く説明します。

質量は（密度）×（体積）で、今回は定常かつ断面積一定なので、進行方向の長さの変化だけ考えて \rho u=一定が質量保存を表します。

運動量は（質量）×（速度）で、質量の方はさっき説明した通り \rho uなので運動量は大体 \rho u^2、力積の変化は圧力変化のみなので式(2)が運動量変化の式を表します。

エネルギーについては、単位体積あたりのエネルギー保存を考えると、運動エネルギーが\dfrac{1}{2}u^2であり、エンタルピーhについては定圧比熱が理想気体では\dfrac{\gamma}{\gamma-1}R（これは比熱比\gammaの定義とマイヤーの関係式からわかる）となることと状態方程式p= \rho R Tからh=\dfrac{\gamma}{\gamma-1}\dfrac{p}{\rho}となることから式(3)がエネルギー保存を表します。

 

以上で説明した三つの保存則を用いて圧力比\dfrac{p_2}{p_1}と密度比\dfrac{\rho_2}{\rho_1}の関係式を求めます。式(1)を二通りの方法で式(2)に代入すると\begin{align}u_1(u_1-u_2)&=\frac{1}{\rho_1}(p_2-p_1)\\ u_2(u_1-u_2)&=\frac{1}{\rho_2}(p_2-p_1)\end{align}

辺々足して

\begin{equation}{u_1}^2-{u_2}^2=(p_2-p_1)\left(\frac{1}{\rho_1}+\frac{1}{\rho_2} \right)\end{equation}

上式と式(3)から{u_1}^2-{u_2}^2を消去して整理すると、目的の式が出てきます。

ランキン・ユゴニオの式 \dfrac{\rho_2}{ \rho_1}=\dfrac{\dfrac{\gamma+1}{\gamma-1}\dfrac{p_2}{p_1}+1}{\dfrac{p_2}{p_1}+\dfrac{\gamma+1}{\gamma-1}}

 

上式のことをランキン・ユゴニオ（Rankine-Hugoniot）の式と言います。この式の導出についてもうちょいよく知りたいという方は空気力学第三の講義（や適当な圧縮性流体の本）へどうぞ。

ja.wikipedia.org

 

・・・いかがでしたか？

ただ三つの保存則連立させただけじゃないかと思った方もいると思います。しかも別に特段綺麗な式でもないし、理想気体に過ぎないし、なんでこんな式にランキンユゴニオ何て名前がついてるのか、わからん！と思った人もいることでしょう。

実は、もっと一般の場合、すなわち非定常な現象、発展方程式に対しても不連続面を考えることもでき、そのときにもランキンユゴニオが出てきます。不連続面前後の関係を表す式のことを一般にランキンユゴニオの式という、みたいな感じです。

では、具体的に非定常な場合はどのように扱うのでしょうか？キーワードは上でも強調した''保存則''です。

保存則、弱解の導入と保存則に対するランキン・ユゴニオ条件

ランキンユゴニオさんに出会う前にいくつか準備をします。文字の定義も一回忘れてください。まず、次式で表すようなu:\mathbb{R} \times\mathbb{R}_+ \ni(x,t)\mapsto u(x,t)\in\mathbb{R}についての偏微分方程式を（スカラーの）保存則と呼びます。

保存則\dfrac{\partial u}{\partial t}+\dfrac{\partial}{\partial x} f(u)=0 \tag{＊}

fは既知関数とします。

スカラーの、とわざわざつけたことからもわかる通り、uが多次元の値を返すような保存則も\dfrac{\partial }{\partial x}を \nabla\cdotに変えるだけで記述できます。ですが多次元版は結構難しいのでこんかいはスカラーを返すものだけ考えましょう。一番簡単な例は一次元移流方程式\begin{equation}\dfrac{\partial u}{\partial t}+c\dfrac{\partial u}{\partial x} =0\end{equation} がありますね。上で示唆したとおり、非定常な流体現象も次のような保存則で記述できます。\begin{align}&\frac{\partial q}{\partial t}+ \nabla\cdot f=0\\&q=\left[\begin{array}{c}\rho\\\rho u\\E\end{array}\right],f=\left[\begin{array}{c}\rho u\\\rho u^2+p\\(E+p)u \end{array}\right]\end{align}いわゆるオイラー方程式のことです。

なぜこれらが保存則と呼ばれるのか、それは保存則の定義から\begin{align}\frac{\mathrm{d}}{\mathrm{d}t}\int_{-\infty}^\infty u\,\mathrm{d}x&=\int_{-\infty}^\infty\frac{\partial u}{\partial t}\,\mathrm{d}x \nonumber\\&=-\int_{-\infty}^\infty\frac{\partial }{\partial x}f(u)\,\mathrm{d}x \nonumber\\&=0\end{align}が成り立つからです。ただし、uに対しては微分と積分の順序交換ができ、かつuはコンパクト台を持つと仮定しました。

このような物理的意味をもつ偏微分方程式が保存則なわけで、「自然界は理想的には滑らかで連続的に決まってる！」なんて思ってしまうと、この偏微分方程式は常に滑らかな解を持ちそうな気がして、不連続面なんて出てこない気もします。しかし、次の命題が示すように、こんな単純な方程式であっても自然に滑らかさが失われてしまうことがあるのです。

命題１f\in C^\infty[a,b]かつfは下に凸とする。保存則(＊)に対し初期条件u(x,0)=u_0を課した初期値問題を考える。ただし、u_0は単調非増加なC^\infty級の関数であって、あるx_{0}\in\mathbb{R}_+が存在して\begin{align}u_0(x)=\begin{cases}b&(x\leq-x_0)\\a&(x\geq x_0)\end{cases}\end{align}となる。このとき、初期値問題の解は有限時刻で滑らかさを失う。□

f:id:nobo0409mathinfo:20191130164334p:plain

u_0のイメージ。ペイントで30秒くらいでつくった。

 証明：

まず、滑らかな解を持つなら一意であることを示します。u_1,u_2を初期値問題を満たす相異なるC^{\infty}級の解であるとして矛盾を導きます。平均値の定理から\begin{equation}f(u_1)-f(u_2)=(u_1-u_2)\int_0^1f'(\theta u_1+(1- \theta)u_2)\,\mathrm{d}\theta\end{equation}が成り立つので、w=u_1-u_2,p=\displaystyle\int_0^1f'(\theta u_1+(1- \theta)u_2)\,\mathrm{d}\thetaとおくと\partial_t w(x,t)+\partial_x(p(x,t)w(x,t))=0,w(x,0)=0となりますが、W=w(X(t),t),\dfrac{\mathrm{d}X(t)}{\mathrm{d}t}=p,X(0)\in\mathbb{R}という特性曲線上の変数変換（速度uで運動している人から見た座標系）を考えると\begin{equation}\begin{cases}\dfrac{\mathrm{d}W}{\mathrm{d}t}+(\partial_x p)W&=0\\W(t=0)&=0\end{cases}\end{equation}という常微分方程式にまで帰着されます。この解は、常微分方程式の解の一意性からW(t)=0であり、X(0)の取り方に依らないので、結局u_1=u_2となってしまい矛盾です。

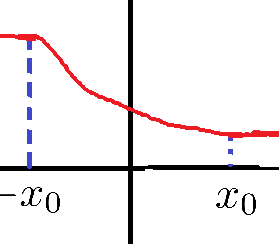
一方、計算によって\begin{equation}v=u_0(x-f'(v)t)\end{equation}が解であることがわかります。さっき解の一意性を保証したので以降はこのvについてだけ考えればよいです。このvの存在と陰関数定理から、tが十分小さいときに解が存在することは言えますが、大域解は存在しえません。なぜならばこのとき\begin{equation}v(x,t)=\begin{cases}b&(x-f'(b)t\lt-x_0)\\a&(x-f'(a)t\gt x_0)\end{cases}\end{equation}となりますが、fが下に凸なことから f'(a) \lt f'(b) であり、x-f'(b)t\lt -x_0かつx-f'(a)t\gt x_0をみたす(x,t)が存在し、u=vが定義されないからです。

以上より主張が得られました。■

今示した命題から、保存則は不連続現象を内在的に引き起こすことがわかりました。つまり有限時間まってると下図のようなjumpが生じてしまうということですね。

f:id:nobo0409mathinfo:20191130223938p:plain

有限時刻なのに不連続、つまりjumpが生じてしまったuのすがた。

それは、方程式(＊)のようなC^1級以上の滑らかな解をあつかっていても無駄であるということでもあります。なので、不連続な解も認めるよう解概念を拡張した方が都合がよさそうです。そのような概念は弱解と呼ばれ、次のように定義されます。

定義１f\in C^\infty(\mathbb{R})、u_0\in L^\infty(\mathbb{R})とする。u\in L^\infty(\mathbb{R} \times[0,T))が保存則\partial_t u+\partial_x f(u)=0 の弱解であるとは\begin{equation}\int_{\mathbb{R} \times[0,T)}(\partial_t\varphi(x,t)\cdot u+\partial_x\varphi(x,t)\cdot f(u))\,\mathrm{d}x\mathrm{d}t+\int_{\mathbb{R}}\varphi(x,0)u\,\mathrm{d}x=0 \nonumber\end{equation}がすべての\varphi\in C_{\mathrm{c}}^1(\mathbb{R} \times[0,T))について成立するときをいう。

 この弱解がちゃんと拡張になっている、つまり、滑らかな解が弱解になっていることは\varphi(\partial_t u+\partial_x f(u))=0の両辺をxとtで積分し、あとは部分積分すれば確認できます。また、衝撃波のような不連続な解も（上の定義式にuの偏微分が含まれてないことに注意すると）扱えるようになっていることがわかります。

 

以上でランキン・ユゴニオ条件が登場する土台が整いました。少し長かったですかね。。。すいません。

ランキン・ユゴニオ条件とは、今定義した弱解が存在する必要十分条件となるような条件のことを言います。その定理を言う前にいくつか言葉を定義しておきます。

f:id:nobo0409mathinfo:20191201003842p:plain

D_lとかの図。

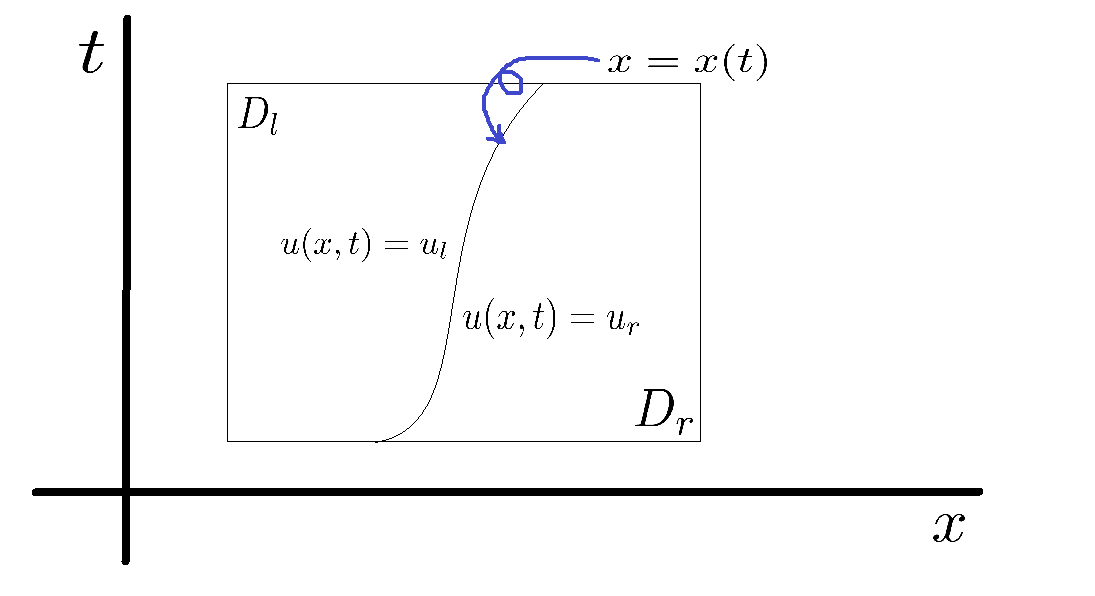
まず上の図で長方形で囲まれている領域をD=(x_0,x_1) \times(t_0,t_1)とし、x=x(t)を特性曲線とします。それとD_l=\left\{(x,t)\in D\mid x\gt x(t)\right\},D_r=\left\{(x,t)\in D\mid x\lt x(t)\right\}とします。また、\begin{align}u_l(t)&=\lim_{D_l \ni(y,s) \to(x(t),t)} u(y,s)\\u_r(t)&=\lim_{D_r \ni(y,s) \to(x(t),t)} u(y,s)\\f_l&=f(u_l)\\f_r&=f(u_r)\end{align}とおきます。

以上の準備のもとで、ランキン・ユゴニオ条件は次のような定理に登場します。

定理１f\in C(\mathbb{R}),u\in C^1(\overline{D}_l),u\in C^1(\overline{D}_r)（x(t)上では連続じゃなくてもよい）とする。uが保存則(＊)の弱解である必要十分条件は、次のランキン・ユゴニオ条件を満たすことである。\begin{equation}\frac{\mathrm{d}x(t)}{\mathrm{d}t}(u_l-u_r)=f_l-f_r\end{equation}□

 証明：

\varphi\in C_{\mathrm{c}}^\infty(D)をとる。i=r,lとして\begin{align}&\int_{D_i}(\partial_t\varphi\cdot u+\partial_x\varphi\cdot f(u)),\mathrm{d}x\mathrm{d}t \nonumber\\=&\int_{\partial D_i}\varphi( \nu_t^iu+ \nu_x^if(u))\,\mathrm{d}\ell \nonumber\\=&\int_{\Gamma}\varphi( \nu_t^iu+ \nu_x^if(u))\,\mathrm{d}\ell \nonumber\end{align}が成り立つ。ただし\Gamma=\left\{(x,t)\in D\mid x=x(t) \right\}で、 \nu^i=( \nu^i_t, \nu^i_x)はD_iの外向き法線ベクトル。よって、uが弱解とすると\begin{align}0&=\int_D(\partial_t\varphi\cdot u+\partial_x\varphi\cdot f(u))\,\mathrm{d}x\mathrm{d}t \nonumber\\&=\left(\int_{D_l}+\int_{D_r} \right)(\partial_t\varphi\cdot u+\partial_x\varphi\cdot f(u))\,\mathrm{d}x\mathrm{d}t \nonumber\\&=\int_\Gamma\left(\varphi(\nu_t^lu_l+ \nu_x^lf_l)+\varphi(\nu_t^ru_r+ \nu_x^rf_r) \right)\,\mathrm{d}\ell \nonumber\\&=\int_\Gamma\left(\varphi(\nu_t^lu_l+ \nu_x^lf_l)-\varphi(\nu_t^lu_r+\nu_x^lf_r) \right)\,\mathrm{d}\ell \nonumber\\&=\int_\Gamma\varphi\left(\nu_t^l\left(u_l-u_r \right)+ \nu_x^l\left(f_l-f_r \right) \right)\,\mathrm{d}\ell \nonumber\end{align}が従います。\varphiは任意なので、変分学の基本補題より\begin{equation}\nu_t^l(u_l-u_r)+ \nu_x^l(f_l-f_r)=0\end{equation}となりますが、\dfrac{ \nu_t^l}{\nu_x^l}=-\dfrac{\mathrm{d}x}{\mathrm{d}t}なので\begin{equation}-\dfrac{\mathrm{d}x}{\mathrm{d}t}(u_l-u_r)+(f_l-f_r)=0\end{equation}となり、ランキン・ユゴニオ条件が満たされます。逆は変分学の基本補題の逆が自明なので上の議論を逆にたどっていけば成り立ちます。■

これでランキン・ユゴニオの正体がようやくわかりました。つまり、ランキン・ユゴニオとは、衝撃波の速度\dfrac{\mathrm{d}x}{\mathrm{d}t}と''保存''量の変化f_l-f_rの関係式のことだったんですね。定常の場合は前者がゼロで、保存量の変化がゼロということで、最初にやったような各種保存量の保存則が出てきたんですね。

渋滞もランキン・ユゴニオで説明できる！？

最後に、今出てきたランキン・ユゴニオ条件を用いてちょっとした応用をしてみたいと思います。題材は航空宇宙で最も有名な教授の一人、我らが西成活裕先生が研究している渋滞、とくに交通流のモデルを扱ってみましょう。設定としては

  1. 一車線のみで車の位置はxで表せる。
  2. 位置xを時刻tに通過する車の数は、車の密度\rho(x,t)と速度v(x,t)を用いて\rho vで与えられる。なので、\rhoについての保存則として、次式が成り立つ。\begin{equation}\frac{\partial\rho}{\partial t}+\frac{\partial}{\partial x}(\rho v)=0\end{equation}。
  3. 車の数が少なければ、車は速く走る。
  4. v=v(\rho)
  5. 車の数が増えると速度が減少する。すなわちvは \rhoの減少関数。
  6. ある密度\rho_{\max}以上になるとv=0

上記を満たすようなvにはいろいろなモデルが提案されていますが、今回は簡単な線形モデル\begin{equation}v=v_{\max}\left(1-\frac{\rho}{\rho_{\max}} \right)\end{equation}（ただしv_{\max}は適当な正定数）を用いてみます。このとき\displaystyle f(\rho)=\rho v_{\max}\left(1-\frac{\rho}{\rho_{\max}}\right)となります。

この交通流が渋滞したとき、つまり、ある時刻t=0でx=0より前では\rho=\rho_r=\rho_{\max}となり、それより後ろでは\rho=\rho_l\lt\rho_{\max}となった状況を考えましょう。式で解の形を記述すると次のようになりますね。\begin{equation}\rho_0=\begin{cases}\rho_{\max}&(x\gt 0)\\ \rho_l&(x<0)\end{cases}\end{equation}

 

f:id:nobo0409mathinfo:20191201042051p:plain

交通流のモデル。http://www.clawpack.org/riemann_book/html/Traffic_flow.htmlより引用

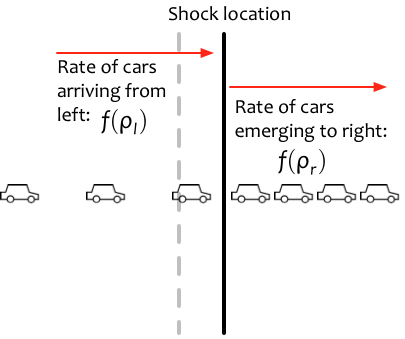
初期条件がこのように与えられた保存則が衝撃波解、弱解を持つ条件がランキン・ユゴニオ条件からわかるのでした。すなわち、衝撃波の速度、渋滞の境目が動く速度は\begin{equation}\frac{\mathrm{d} x}{\mathrm{d} t}=\frac{f(\rho_l)-f(\rho_r)}{\rho_l- \rho_{r}}=-\frac{ \rho_{l}v_{\max}}{\rho_{\max}}\lt0\end{equation}となります。

ここからわかるのは渋滞の境目は後ろに進んでいくということです。数式で言われても。。。という方も多いと思うので、次の動画で実際に実験してみた様子をご覧ください。

たしかに渋滞は後ろに伝わっていきます！これはちょっと感動しませんか？？？笑

まとめ

ここまで読んでいただいた方、ありがとうございました。多分読み飛ばしてここまで来た方もいらっしゃると思うので、この記事の内容をまとめておくと

まとめ圧縮性流体力学の入門として扱われるランキン・ユゴニオ関係式は、保存則という観点、そして、衝撃波を弱解で扱うという工夫により、一般に不連続面（衝撃波）の速度と"保存"量変化の関係を表し、その一般化によって渋滞現象の解析も可能となる。

 って感じです。

できれば保存則の数値計算についてもお話ししたかったのですが、この記事を書いていたら12月になってしまったので今日はこの辺で。読んでいただきありがとうございました。

これ以降のアドベントカレンダーの記事はもっと面白いと思うので、お時間ある方は是非毎日見ていってくださいな。

それでは、素敵な12月をお過ごしください～～～

航空宇宙から数理情報に進学する体験談③入試当日：専門科目（数理情報学）

おはこんばんにちは。真空です。今日は久しぶりに熱い日でしたね。こんな日はクーラーの効いた部屋にこもってブログを書いたり本読んだりするのがいいかもしれませんね。

 

今日は8/20(火)におこなわれた数理情報学専攻の専門科目：数理情報学の試験当日の様子を振り返っていきたいと思います。

試験前日

共通数学の試験が終わり、19時くらいまで寝ていた。寝たおかげで何とか気分を切り替えられたので、一昨日までに頭の中で作っておいた専門科目に出る気がするリストの復習をすることにした。予想した内容は

  1. DM分解（某計数民のブログの影響）
  2. 実三重対角行列の固有値問題が分割統治でとけるはなし
  3. FFT
  4. Euclid復号
  5. EMアルゴリズムやGibbs Samplingの導出っぽいやつ
  6. Pfaffianとマッチング
  7. 単体法、特にネットワークシンプレックス法
  8. Cahn–Hilliard方程式の構造保存数値解法

って感じだった。数理情報の院試は毎年ストーリーの異なる問題が出るので、予想を的中させるのは難しいが、その分「どんな問題出るのかな～～」と妄想を膨らませることができるので楽しいといえば楽しいし色んな論文を垣間見したりできるので研究にも役立ちそう。

そのあとは数値解析入門のQR分解とLU分解、LDL分解の項の証明と演習問題を軽くやりなおして、21時くらいに帰宅し就寝。

www.utp.or.jp

試験当日：試験直前

昨日の反省を活かして、ちゃんとよく眠れたと体が判断できた時刻に起きようと思い、7時くらいに起床。ラボに行き、朝食のおにぎりを食べ、好きな音楽を聴きながら適当にいままで読んできた本たちを流し見る。この証明でそうだなーとおもった命題を2つほど証明したらいい感じの時間になったので試験会場に向かう。すでに友人たちが入室していたので、昨日同様ダル絡みしにいく。めっちゃ緊張していたり逆に数理情報学をすべて理解したといわんばかりのひともいて、さまざまな受験勉強の仕方があったんだなあとおもった。そうしているうちに試験監督の方々が入ってきたので着席し、解答用紙3枚*1と問題冊子を受け取り、注意等を聞いたのち試験開始。

試験当日：試験中

とりあえず全問確認してどの問題を選択するか決めることにする。

  • 第一問：工学教程の線形代数Iでみたやつじゃん！（進研ゼミ風）と思い、とりあえず選択しようと思う
  • 第二問：よく出る指数分布じゃん！（進研ry）と思うも、値が小さいときは観測できないというように変形されている。問２までは解けそうだが問３がぱっと見ではよくわからない。保留
  • 第三問：多項式環でた！ヤマ当たった！！と思うも、なんだか2n変数多項式環からn変数有理関数体への凖同型写像を考えていて見たことない感じになっている。問１は簡単そうだが問２でxy-1というイデアルを考え始めている。アティマクの最初の方にのっていたようなイデアルな気がしたが、アティマクを読んでいないので不安になる。初めて出題される分野なので難しくはないのかもしれないが、とりあえず保留。
  • 第四問：半離散近似だし離散フーリエ変換じゃん！数値計算じゃん！！と思い志望分野的にも力入れて勉強した分野的にもこれは解かなアカン、と思ったので解くことにする。
  • 第五問：配列についてのなんかだなあと思う（こなみ）。アルゴリズムとデータ構造から出題されたら離散最適化の問題が出ない限り競技プログラミング勢に敵わないなあと思ったので解くのはよしておこうと前々から思っていた。ので解かないことにした。

以上の観察から１⇒４⇒（２xor３）という風に手を付けていくことにした。

第一問

文字の置き方は忘れたが、簡単に言うと制御で出てくるLyapunov方程式CX+XC=Bの解の存在、および一意性の証明が問１、問２はCとXが可換であることとCとBが可換であることが同値であることの証明だった（気がする）。工学教程でSylvester方程式を扱ったときはテンソル積の形に直して示していたのでその方針で変形していい感じに問１を示し、問２も対角化したりして丁寧に両方向示す。統計で線形モデルを扱う際にもテンソル積（の基底に関する表現行列）を用いたりしたので、過去問にはなかったけどやっといてよかった～などと思いながら見直し、大丈夫だと確信してから次の問題へ移る。ここまでで45分経過くらい。

第四問

問題の設定は周期境界条件を課した一次元熱方程式を空間に関してのみ離散化したときの解を誘導に乗りながら構成し、離散化してもちゃんと熱方程式の構造を保存すること、すなわち時刻無限大で熱が一様に分布することを確かめる問題。いかにもmto先生の出題なので完璧に解かなければならないというプレッシャーがかかる。問１はu(n,t)=c_n\exp\left(\mathrm{i\pi}\frac{nm}{N}\right)みたいな形を仮定したときの解を求める問題なので簡単。問２はこの偏微分方程式を解けという問題だった。離散フーリエ変換だというのと問１で基準振動解を出したことからとりあえず解をエスパーして構成し、それが解となることと一意性を示そうという方針をたて、解答を書こうとするも係数の調整に謎に時間がかかってしまう。なんとか係数を合わせ、解であることを示したが、今度は一意性の証明が微妙だなあと思うも、初期条件がゼロならODEで考えたらまあそうだよな、みたいなノリで日本語を書いて一意性を示す。ここまで出来たら極限を求める問３は簡単。有限和ありがとうという気持ちになりながら見直しをし、次の問題へ移る。ここまでで２時間経過くらい。ちなみに、あとで同クラに聞いたら三重対角行列の固有値固有ベクトルを問１で求めていることに気づくと離散フーリエ変換であることに気づかなくても自然に解けるらしい。確かに過去の傾向から言ってもそっちの方がよさそう。

 

第二問

第三問と迷ったが、志望教員に代数の先生を書いてないというのが決定打になり第二問の確率を解くという選択をとる。直前は確率統計より代数をやったけど、受験勉強全体で見たら確率の方がやったし、多少はね？

問題の設定は実測値がa以下であるときはすべてaという観測値をとってしまうような指数分布について、問１はその期待値、問２はその期待値がある値（忘れた）になるような\lambdaが一意に存在することの証明で、そこまでは比較的容易であったが、問３でこのような特殊な指数分布の畳み込みの密度関数を求めよ的なことを要求されて困惑する。一般に指数分布の畳み込みはガンマ分布になるが、今回はただの指数分布じゃないから特性関数もよくわからん（わかるがその積を考えたところでなにもわからなそう、というかガンマ分布の特性関数覚えてねえ）という感じで特性関数をつかういつもの手法が使えなさそうなのが痛い。とりあえず順序統計量の分布関数を求めるときのノリで分布関数を求める方針で計算することにする。計算をはじめてはみたものの、積分区間がいつもより汚い形なので全然綺麗にならない。なんとか積分の残らない形で書いたものの和が残ってしまう。汚いものの、計算の方針的には間違っていないはずなのでこれで解いたことにする。問４はこの密度関数が最大値を持ち、それを達成するxが一意であることを示す問題だったが、自分の持ってる問３の答えが汚くて無理じゃね？という気持ちになる。とりあえず微分したらただの多項式を考えればよいだけになることは分かったので、その多項式をいい感じに変形していい感じの日本語を添えて体裁を整えておく。問３の導出をもう一度見直すも、やっぱりわからないのでガバガバのまま問４の解答を終えることにする。

そのあと大問三つ全てを見直すフェーズに入る。記法について何も述べていなかったので一応空いたスペースに記法の説明をしておく。そんなことをしていたら試験終了。お疲れさまでした。

試験終了後

流れで計数の控室にいき、しばらく試験について駄弁り傷をなめあう。そのあとご飯食べに行ったりスマブラしたりしてゆっくりしたのち一時帰宅。口述試験のためにYシャツクリーニング＆新調しようと思い上野に行き、その帰りに一人で天気の子を観に行く。とても感動した。

*1:ちなみに解答用紙の大きさは定期試験の時と同じで、解答した番号と受験番号を記載する欄以外は真っ白だった。なので解答が書ききれないということは（裏面も使えるので）ないと思う。まだ自分の得点が届いていないので去年までの噂でしかないが、数学の試験なので当然証明に必要十分な要素はちゃんと記述しないとどんどん減点されていくらしい。なので裏面も積極的に使用できる

航空宇宙から数理情報に進学する体験談②入試当日：共通数学

みなさんおはこんばんにちは。真空です。今日は生憎の曇り空ではありますが、涼しくなってて過ごしやすい一日となりそうですね。

 

今日は8/19(月)におこなわれた情報理工学系共通試験科目：数学の当日の様子を振り返りたいと思います!なお問題の詳細についてはよく覚えてなかったりするのであとで公表されるであろう問題を見てください。

 

試験前日

前日は午前は普通に専門科目の勉強（多分線形計算の数理

www.iwanami.co.jp

あたりを読んでいた）をし、午後は二日前くらいにやった去年の過去問を解きなおした。そしたら第三問の確率の問題でまた計算ミスをしてテンションが下がったのでふて寝したら17時くらいになっていてさすがにちょっと焦った。一度解いた問題を解きなおすと精神衛生上よくないと気付いたので、数値計算法の数理

www.iwanami.co.jp

のFFTの項を新たに読むことにした。代数と解析がちょっとコラボレーションしてるのをみて初心に帰る。そういえばぼくはこういうことに素直に感動して数（理工）学が好きになったんだった。入試本番前に思い出せてよかった、とおもったらかなり落ち着いた。その日は20時くらいの早めの帰宅、21時くらいに小学生並みの早さで床に就いた。が、なんだか目がさえてしまって寝つきがよくなかった。

 

試験当日：試験直前

6時ごろ起床、ちょっと寝不足感があった。とりあえず大学に行き、100円ローソンで朝食を購入してラボに行って食べる。そのあと、ことしはもっと普通に有名確率分布の期待値や分散や高次モーメントを求める問題がでるやろｗと山を張り、指定参考書にもなっている確率と確率過程

www.asakura.co.jp

をみて特性関数の導出を復習した。一応複素積分がでてくるので導出をちゃんと書こうとするのは面倒だなとおもい、少し焦ったが、まあ共通数学なら形式的に積分しても許されるやろと思い込むことにした。

そうこうしているうちに試験開始30分前になったので試験会場である法文2号館に向かい、適当な知り合いと緊張を解し合ってたら10分前になっていたので着席し、しばらくしたら問題用紙と解答用紙が配られいよいよ緊張してくる。試験開始。

試験当日：試験中

試験開始のアナウンスとともに問題用紙を開く。今考えるとこの時点でかなり焦りがあった。とりあえず大問三つ分をパラパラ眺める。第一問は前半は新規性のない固有値求めたり行列のn乗やexpを求める問題だったが後半が歪対称行列に関する証明問題だった。歪対称行列については専門科目で印象的な問題があったのである程度は準備してきたけど別にあそこまで歪対称行列まわりのFactを知らなくても問題なさそう。だけど計算ミスがこわいな。第二問はまさかの平面上の微分幾何（？）。3Aセメスターにとった数学３の内容覚えてるかな、、、と少し不安になる。第三問は日本語が長いからあとでじっくり読んだ方がよさそう。以上みたいなことを5分程度でおもったのち、普通に第一問から取り掛かることにした。

第一問

とりあえず固有対をもとめる。ここで落としてはいけないと思い検算をしたのはよかったのだが、緊張しすぎたのか(A-\lambda I)u=0を確認しているつもりだったのにAu=0を確認していて10分強時間を無駄にする。この時点でかなり嫌な予感がするも、そのあとは検算の検算を心がけることができたのでキチンと答えに自信を持ちながら計算できた。後半の論証はちょっと時間を使いすぎたなという感じだったので\sin,\cosのTaylor展開の導出やそれらを正n角形上で足すと0とか1になるやつの証明はかなり雑に書いたが、高校数学だし許されていると信じて解答を書く。仕上がったので次の問題へ進む。

第二問

数学３の最初法でやったやつだ！（進研ゼミ感）とおもうも、微妙に違うことに気づく。あとどこまで正確に論証したらいいかわからなかった。とりあえずごりごり微分したりしてなんとか嘘はつかないようにした。ただ、途中で「～～～がなりたつことを説明せよ」という問題があって、厳密な証明は求めてないんだろうけど、だとしたら何を言っても正解じゃね？と思い困惑した。とりあえずそれらしいことをいって丸をもらったつもりになっておく。最後に一般の凸図形から距離rだけ離れた領域に関する積分公式を導出するのはすこし興味深かった。

第三問

この大問に辿り着いた時点で残り時間は1時間くらいだった。まだ余裕があるなと思いじっくり問題文を読んでみる。するとなんか高校数学の美しい物語とかで見たことあるネタだなあということに気づく。

mathtrain.jp

そう思った瞬間、この問題は完答しなければいけないという焦りが生まれてしまい、しかもなぜか問一と問二の答えの辻褄が合わなくてさらに焦ってしまった。そこから30分ほとんど何も考えることができず、このままだとマジで落ちるとおもったらもう何も考えられなくなってしまった。とりあえず最後の小問の後半は-x\log xの最大値を求めるだけだったのでとりあえず書いておく。その後問二に戻るも何が間違えているかさっぱりわからない。これはまずいと思い、（ここで初めて）問三以降の問題をみてみると、なんと問一と問二を一般化してる問題になっているじゃありませんか。しかもものすごいヒントとなってる問題があって、なんで最初からこっちまで目を通しておかなかったんだ……誘導下手くそかよ…と作問者を恨む時間もなく、とりあえず問三をヒントに問二を書き上げ、問二と同様の理屈で～ということで問三と問四を解いた感じを装って解答を書き上げ、問五はなんかいい感じに漸化式を導出して瞬殺し（これも最初にやっておけばよかった……）、最後の小問の前半はまたもや「～説明せよ」とガバガバ指定だったのでガバガバな解答を書いてとりあえず解答の体裁を整える。これでのこり3分くらいになったので全体をザーッと見直す。試験終了。手汗めっちゃ掻いた。

試験後

数理情報受験者は大事なお知らせがあるということなので工６にいくと、新しい教員が志望できるようになったとのことだった。とてもいいなあと思う先生が一人いたので、第6志望に加えさせていただいた。

それがおわりいろいろな知り合いといろいろ話したのち、いつもの勉強部屋に帰還。すぐに翌日の専門科目の対策を始めようとしたが、試験で相当に疲れていたのか、生まれて初めて勉強中に寝落ちて本を汚してしまうという失態を犯した。専門科目が不安になる…

 

to be continued......

航空宇宙から数理情報に進学する体験談①入試当日：TOEFL ITP

みなさんおはこんばんにちは。真空です。九月が始まって少し暑さが和らぐ日もでてきたりでてこなかったりラジバンダリ*1。

……

今回のお品書きは次のようになっております。 

では早速まいりましょう。

院試体験談執筆予定

今回から何回かに分けて2020年度東京大学情報理工学系研究科数理情報学専攻入学試験について書いていきたいと思います。予定では全14回を予定しています。内容は以下の通り（の予定）。

  1. 入試当日①（今回）：TOEFL
  2. 入試当日②：共通数学
  3. 入試当日②：専門科目（数理情報学）
  4. 院試勉強スケジュール
  5. 過去問について
  6. 院試のために勉強した本①線形代数
  7. 勉強した本②解析、数値解析
  8. ③最適化
  9. ④確率・統計
  10. ⑤代数
  11. ⑥離散数学、アルゴリズム
  12. ⑦幾何
  13. ⑧英語
  14. ⑨（番外編）航空宇宙工学

こうやって書くと意外と書くこと多くなっちゃいそうですね。冗長にならないよう気を付けます。

まずは記憶がまだ新しいうちに入試当日のことから書いていきます！今回は8/6に行われたTOEFL ITPについて振り返っていきたいと思います。

TOEFL　ITP

一か月前くらいに受験した模試は537点でザ・普通って感じだったので、これより15点、できれば20点多く得点したいなあと思いながら、前日はずっとつかってきた駿台の参考書((

bookclub.japantimes.co.jp

)))のリスニング部分を聞き流しながら22時ごろ帰宅し就寝。次の日は8時起床。試験開始は午後からだったので、とりあえずいつも勉強していた航空の入試専用自習部屋にいき朝ごはんを食べながらもう一回リスニングを聞き流す。初見のときは全然聞き取れなかった音声が（覚えちゃったというのもあるけど）かなりわかるようになっている、と、思い込ませることによってとりあえず自信をもつことに成功する。

 

ご飯を食べたら眠くなったので、気分転換に専門科目の勉強を1時間くらいする。そうしていると学科民がはいってきて眠気が飛んだので文法の復習をはじめた。

 

そうこうしているうちにお昼の時間、おにぎり一個と魔剤半缶分を胃に流し込む。これでリスニング0点は免れた。

ご飯を食べて落ち着いたら試験会場である法文一号館へ。なんかたくさん受験者がいてビビるが、友達にダル絡みして無理やり落ち着かせる。

そうこうしている間に席に着席するように言われたので素直に従い、30分間みんなで仲良く名前や受験番号を書く。この虚無タイムにより試験間際に細かい文法を詰め込んでもすべて忘れてしまうので、ITPに関しては直前にガンガン文法書を読む必要はないと思う。むしろちょっとわかんなくても即断即決できるようアタマを柔らかくしていくのが必要。

この虚無タイムが終わり、7分程度のトイレ休憩の後試験開始、約二時間の間休みなく問題を解く（実際は文法と長文に関しては多少時間が余ると思うのでそこで休める）。

最初のリスニングではいつも通りPart １の短い会話のやつで意外と手間取る。選択肢をじっくり吟味してしまうと次の問題が流れてくるし、かといってあんまりにも即断してしまうと罠選択肢に引っ掛けられたりするので難しい。さらに一応入試本番であるという緊張で余計焦ってしまった。感触は模試より微妙という感じか。

そのあとの文法と長文に関しては駿台の参考書と似た感じの問題がいくつかあったきがしたので模試の時よりはかなりできたと思う。

 

そんなかんじで一喜一憂しながら問題を解いていたら試験終了。全体的な感触としては前よりは絶対できたという感じ。試験終了後はこれでようやく数学だけしてれば許されるという解放感からか白くまアイスを食べながらしばらくぼーっと次回の院試ゼミで自分が担当する問題を眺めてしまう。その後院試勉強中（可算）無限に通った本三スタバ近くの四川料理の店で刀削麺を食べラボに帰宅。しばし微睡んだ後、先程アイスを食べながら練った解答をTeX打ちしてたら夜が明けてしまった。その後自宅に帰り7時頃就寝した（気がする。）。

*1:

dic.nicovideo.jp

ブログ、はじめました。

皆さんはじめまして。真空と申します。

軽く自己紹介すると、航空宇宙工学科に所属する大学４年生です。つい最近数理情報学専攻の院試に受かったので、（入学手続きと卒論と卒業設計をミスらないかぎり）春から数値解析学を専攻していくことになっています。

そういうわけで、まずは航空から数理情報にいった経験を残しておいたほうがいいだろうというのと、大学院で専門を変更するにあたり基礎的な解析学の知識や計算機の扱い、あとは数値解析の専門家が新規参入できそうな応用分野をまとめておこうとおもい、このブログを開設するに至りました。

最初の方は院試体験談を何回かに分けて書いていくつもりなので、よろしくお願いします。