ランキン・ユゴニオってそんなに大事？～圧縮性流体入門から保存則の偏微分方程式論、そして渋滞へ～

おはこんばんにちは。卒論やってたら更新がめっちゃ遅くなってしまいました、ごめんなさい（土下座）。ブログ続けるのってむずかしい・・・

今日は東京大学航空宇宙アドベントカレンダー2019一日目ということで、タイトルにもある通り、航空宇宙ゴリゴリ、かつ今の研究にちょっと関連する話（できれば来年の研究にも）の内容を書きたいと思います。

adventar.org

（院試勉強関連の話は春休みくらいに再開するつもりなのでしばしお待ちください。）

最初に要旨をまとめておくと

圧縮性流体の一番最初に''定常な''垂直衝撃波（不連続面）前後の物理量を関係づけるRankine-Hugoniotの式を習いますが、なんで名前が付いてる（ほど重要な）のかわからん
実は、ある特殊なクラスの発展（''非定常''）方程式（保存則：Conservation law）が不連続解を持つ条件のことをランキン・ユゴニオ条件という！
ランキン・ユゴニオ条件の観点から車の渋滞現象をみてみるとちょっと面白い。

という感じです。

そんなわけで今日のお品書きは☟みたいになってます。

圧縮性流体力学超入門～Rankine-Hugoniot 関係式導出～
保存則、弱解の導入と保存則に対するランキン・ユゴニオ条件
渋滞もランキン・ユゴニオで説明できる！？
まとめ

では内容に入っていきましょう。

圧縮性流体力学超入門～Rankine-Hugoniot 関係式導出～

まずは航空宇宙らしく、圧縮性流体力学の入門からやりましょう。音速より速い流体の運動、つまり超音速流れでは圧力や密度が不連続変化する現象が見られます。この不連続変化する面を衝撃波といいます。

f:id:nobo0409mathinfo:20191129175706j:plain — シュリーレン法により撮影された衝撃波。wikiより転載。シュリーレン法は院試に出てましたね。

衝撃波の中でも、伝播方向に対して波面（不連続面）が垂直になっているものを垂直衝撃波といいます。垂直じゃないやつは斜め衝撃波です（上図）。単純ですね。斜め衝撃波は式が無駄にめんどいので、以下では次の図にあるような垂直衝撃波を考えます。 $P$ は圧力、 $\rho$ は密度、 $u$ は衝撃波進行方向速度（そうでない方向は今回考えない）、 $T$ は温度、 $M$ はマッハ数です。

f:id:nobo0409mathinfo:20191129182303g:plain — 垂直衝撃波（SW）前後の物理量。http://www.ipc.tohoku-gakuin.ac.jp/simlab/fegs/prog12d.html から引用。

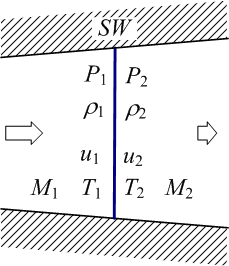
連続（もっと強くいえば微分可能な）な現象であれば運動方程式などの微分方程式をもちいて時間発展を逐一追っていくことによって任意の時刻の物理量を求めることができます。しかし、今回は不連続な面が存在するので、そのような方法はうまくいきません。

こういう状況は高校物理だと物体の二体衝突の問題なんかがありました。そのときはどうしたかというと運動量保存則（と反発係数に関する式）を用いたのでした。今回もそのような保存則を用いる発想で衝撃波前後の物理量の変化、特に圧力比 $\dfrac{p_2}{p_1}$ と密度比 $\dfrac{\rho_2}{\rho_1}$ の関係式を求めてみましょう。

不連続面は薄いとして、断面積の変化・摩擦・熱の流入出がないと仮定します。この状況で成り立つ保存則は以下の三つです。

質量保存則\begin{equation} \rho_1u_1= \rho_2u_2\end{equation}
運動量保存則\begin{equation} p_1+ \rho_1{u_1}^2=p_2+ \rho_2 {u_2}^2 \end{equation}
エネルギー保存則\begin{equation} \frac{\gamma}{\gamma-1}\frac{p_1}{ \rho_1}+\frac{1}{2}u_1^2=\frac{\gamma}{\gamma-1}\frac{p_2}{ \rho_2}+\frac{1}{2}u_2^2 \end{equation}

いきなりこの式書かれても、、、と思う方もいると思うので軽く説明します。

質量は（密度）×（体積）で、今回は定常かつ断面積一定なので、進行方向の長さの変化だけ考えて $\rho u=$ 一定が質量保存を表します。

運動量は（質量）×（速度）で、質量の方はさっき説明した通り $\rho u$ なので運動量は大体 $\rho u^2$ 、力積の変化は圧力変化のみなので式 $(2)$ が運動量変化の式を表します。

エネルギーについては、単位体積あたりのエネルギー保存を考えると、運動エネルギーが $\dfrac{1}{2}u^2$ であり、エンタルピー $h$ については定圧比熱が理想気体では $\dfrac{\gamma}{\gamma-1}R$ （これは比熱比 $\gamma$ の定義とマイヤーの関係式からわかる）となることと状態方程式 $p= \rho R T$ から $h=\dfrac{\gamma}{\gamma-1}\dfrac{p}{\rho}$ となることから式 $(3)$ がエネルギー保存を表します。

以上で説明した三つの保存則を用いて圧力比 $\dfrac{p_2}{p_1}$ と密度比 $\dfrac{\rho_2}{\rho_1}$ の関係式を求めます。式 $(1)$ を二通りの方法で式 $(2)$ に代入すると\begin{align}u_1(u_1-u_2)&=\frac{1}{\rho_1}(p_2-p_1)\\ u_2(u_1-u_2)&=\frac{1}{\rho_2}(p_2-p_1)\end{align}

辺々足して

\begin{equation}{u_1}^2-{u_2}^2=(p_2-p_1)\left(\frac{1}{\rho_1}+\frac{1}{\rho_2} \right)\end{equation}

上式と式 $(3)$ から ${u_1}^2-{u_2}^2$ を消去して整理すると、目的の式が出てきます。

ランキン・ユゴニオの式 $\dfrac{\rho_2}{ \rho_1}=\dfrac{\dfrac{\gamma+1}{\gamma-1}\dfrac{p_2}{p_1}+1}{\dfrac{p_2}{p_1}+\dfrac{\gamma+1}{\gamma-1}}$

上式のことをランキン・ユゴニオ（Rankine-Hugoniot）の式と言います。この式の導出についてもうちょいよく知りたいという方は空気力学第三の講義（や適当な圧縮性流体の本）へどうぞ。

ja.wikipedia.org

・・・いかがでしたか？

ただ三つの保存則連立させただけじゃないかと思った方もいると思います。しかも別に特段綺麗な式でもないし、理想気体に過ぎないし、なんでこんな式にランキンユゴニオ何て名前がついてるのか、わからん！と思った人もいることでしょう。

実は、もっと一般の場合、すなわち非定常な現象、発展方程式に対しても不連続面を考えることもでき、そのときにもランキンユゴニオが出てきます。不連続面前後の関係を表す式のことを一般にランキンユゴニオの式という、みたいな感じです。

では、具体的に非定常な場合はどのように扱うのでしょうか？キーワードは上でも強調した''保存則''です。

保存則、弱解の導入と保存則に対するランキン・ユゴニオ条件

ランキンユゴニオさんに出会う前にいくつか準備をします。文字の定義も一回忘れてください。まず、次式で表すような $u:\mathbb{R} \times\mathbb{R}_+ \ni(x,t)\mapsto u(x,t)\in\mathbb{R}$ についての偏微分方程式を（スカラーの）保存則と呼びます。

保存則 $\dfrac{\partial u}{\partial t}+\dfrac{\partial}{\partial x} f(u)=0 \tag{＊}$

$f$ は既知関数とします。

スカラーの、とわざわざつけたことからもわかる通り、 $u$ が多次元の値を返すような保存則も $\dfrac{\partial }{\partial x}$ を $\nabla\cdot$ に変えるだけで記述できます。ですが多次元版は結構難しいのでこんかいはスカラーを返すものだけ考えましょう。一番簡単な例は一次元移流方程式\begin{equation}\dfrac{\partial u}{\partial t}+c\dfrac{\partial u}{\partial x} =0\end{equation} がありますね。上で示唆したとおり、非定常な流体現象も次のような保存則で記述できます。\begin{align}&\frac{\partial q}{\partial t}+ \nabla\cdot f=0\\&q=\left[\begin{array}{c}\rho\\\rho u\\E\end{array}\right],f=\left[\begin{array}{c}\rho u\\\rho u^2+p\\(E+p)u \end{array}\right]\end{align}いわゆるオイラー方程式のことです。

なぜこれらが保存則と呼ばれるのか、それは保存則の定義から\begin{align}\frac{\mathrm{d}}{\mathrm{d}t}\int_{-\infty}^\infty u\,\mathrm{d}x&=\int_{-\infty}^\infty\frac{\partial u}{\partial t}\,\mathrm{d}x \nonumber\\&=-\int_{-\infty}^\infty\frac{\partial }{\partial x}f(u)\,\mathrm{d}x \nonumber\\&=0\end{align}が成り立つからです。ただし、 $u$ に対しては微分と積分の順序交換ができ、かつ $u$ はコンパクト台を持つと仮定しました。

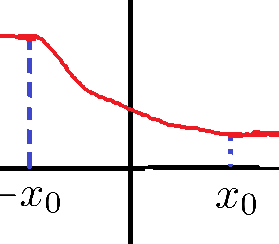
このような物理的意味をもつ偏微分方程式が保存則なわけで、「自然界は理想的には滑らかで連続的に決まってる！」なんて思ってしまうと、この偏微分方程式は常に滑らかな解を持ちそうな気がして、不連続面なんて出てこない気もします。しかし、次の命題が示すように、こんな単純な方程式であっても自然に滑らかさが失われてしまうことがあるのです。

命題１ $f\in C^\infty[a,b$ ]かつ $f$ は下に凸とする。保存則(＊)に対し初期条件 $u(x,0)=u_0$ を課した初期値問題を考える。ただし、 $u_0$ は単調非増加な $C^\infty$ 級の関数であって、ある $x_{0}\in\mathbb{R}_+$ が存在して\begin{align}u_0(x)=\begin{cases}b&(x\leq-x_0)\\a&(x\geq x_0)\end{cases}\end{align}となる。このとき、初期値問題の解は有限時刻で滑らかさを失う。□

f:id:nobo0409mathinfo:20191130164334p:plain — $u_0$ のイメージ。ペイントで30秒くらいでつくった。

証明：

まず、滑らかな解を持つなら一意であることを示します。 $u_1,u_2$ を初期値問題を満たす相異なる $C^{\infty}$ 級の解であるとして矛盾を導きます。平均値の定理から\begin{equation}f(u_1)-f(u_2)=(u_1-u_2)\int_0^1f'(\theta u_1+(1- \theta)u_2)\,\mathrm{d}\theta\end{equation}が成り立つので、 $w=u_1-u_2,p=\displaystyle\int_0^1f'(\theta u_1+(1- \theta)u_2)\,\mathrm{d}\theta$ とおくと $\partial_t w(x,t)+\partial_x(p(x,t)w(x,t))=0,w(x,0)=0$ となりますが、 $W=w(X(t),t),\dfrac{\mathrm{d}X(t)}{\mathrm{d}t}=p,X(0)\in\mathbb{R}$ という特性曲線上の変数変換（速度 $u$ で運動している人から見た座標系）を考えると\begin{equation}\begin{cases}\dfrac{\mathrm{d}W}{\mathrm{d}t}+(\partial_x p)W&=0\\W(t=0)&=0\end{cases}\end{equation}という常微分方程式にまで帰着されます。この解は、常微分方程式の解の一意性から $W(t)=0$ であり、 $X(0)$ の取り方に依らないので、結局 $u_1=u_2$ となってしまい矛盾です。

一方、計算によって\begin{equation}v=u_0(x-f'(v)t)\end{equation}が解であることがわかります。さっき解の一意性を保証したので以降はこの $v$ についてだけ考えればよいです。この $v$ の存在と陰関数定理から、 $t$ が十分小さいときに解が存在することは言えますが、大域解は存在しえません。なぜならばこのとき\begin{equation}v(x,t)=\begin{cases}b&(x-f'(b)t\lt-x_0)\\a&(x-f'(a)t\gt x_0)\end{cases}\end{equation}となりますが、 $f$ が下に凸なことから $f'(a) \lt f'(b)$ であり、 $x-f'(b)t\lt -x_0$ かつ $x-f'(a)t\gt x_0$ をみたす $(x,t)$ が存在し、 $u=v$ が定義されないからです。

以上より主張が得られました。■

今示した命題から、保存則は不連続現象を内在的に引き起こすことがわかりました。つまり有限時間まってると下図のようなjumpが生じてしまうということですね。

f:id:nobo0409mathinfo:20191130223938p:plain — 有限時刻なのに不連続、つまりjumpが生じてしまった $u$ のすがた。

それは、方程式(＊)のような $C^1$ 級以上の滑らかな解をあつかっていても無駄であるということでもあります。なので、不連続な解も認めるよう解概念を拡張した方が都合がよさそうです。そのような概念は弱解と呼ばれ、次のように定義されます。

定義１ $f\in C^\infty(\mathbb{R})$ 、 $u_0\in L^\infty(\mathbb{R})$ とする。 $u\in L^\infty(\mathbb{R} \times[0,T))$ が保存則 $\partial_t u+\partial_x f(u)=0$ の弱解であるとは\begin{equation}\int_{\mathbb{R} \times[0,T)}(\partial_t\varphi(x,t)\cdot u+\partial_x\varphi(x,t)\cdot f(u))\,\mathrm{d}x\mathrm{d}t+\int_{\mathbb{R}}\varphi(x,0)u\,\mathrm{d}x=0 \nonumber\end{equation}がすべての $\varphi\in C_{\mathrm{c}}^1(\mathbb{R} \times[0,T))$ について成立するときをいう。

この弱解がちゃんと拡張になっている、つまり、滑らかな解が弱解になっていることは $\varphi(\partial_t u+\partial_x f(u))=0$ の両辺を $x$ と $t$ で積分し、あとは部分積分すれば確認できます。また、衝撃波のような不連続な解も（上の定義式に $u$ の偏微分が含まれてないことに注意すると）扱えるようになっていることがわかります。

以上でランキン・ユゴニオ条件が登場する土台が整いました。少し長かったですかね。。。すいません。

ランキン・ユゴニオ条件とは、今定義した弱解が存在する必要十分条件となるような条件のことを言います。その定理を言う前にいくつか言葉を定義しておきます。

f:id:nobo0409mathinfo:20191201003842p:plain — $D_l$ とかの図。

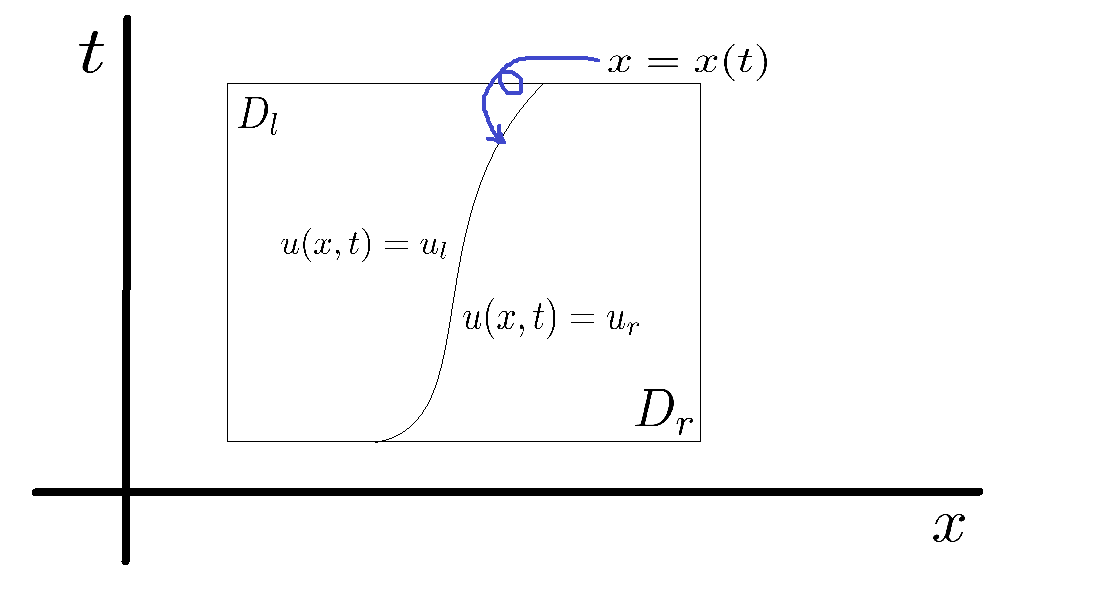
まず上の図で長方形で囲まれている領域を $D=(x_0,x_1) \times(t_0,t_1)$ とし、 $x=x(t)$ を特性曲線とします。それと $D_l=\left\{(x,t)\in D\mid x\gt x(t)\right\},D_r=\left\{(x,t)\in D\mid x\lt x(t)\right\}$ とします。また、\begin{align}u_l(t)&=\lim_{D_l \ni(y,s) \to(x(t),t)} u(y,s)\\u_r(t)&=\lim_{D_r \ni(y,s) \to(x(t),t)} u(y,s)\\f_l&=f(u_l)\\f_r&=f(u_r)\end{align}とおきます。

以上の準備のもとで、ランキン・ユゴニオ条件は次のような定理に登場します。

定理１ $f\in C(\mathbb{R}),u\in C^1(\overline{D}_l),u\in C^1(\overline{D}_r)$ （ $x(t)$ 上では連続じゃなくてもよい）とする。 $u$ が保存則(＊)の弱解である必要十分条件は、次のランキン・ユゴニオ条件を満たすことである。\begin{equation}\frac{\mathrm{d}x(t)}{\mathrm{d}t}(u_l-u_r)=f_l-f_r\end{equation}□

証明：

$\varphi\in C_{\mathrm{c}}^\infty(D)$ をとる。 $i=r,l$ として\begin{align}&\int_{D_i}(\partial_t\varphi\cdot u+\partial_x\varphi\cdot f(u)),\mathrm{d}x\mathrm{d}t \nonumber\\=&\int_{\partial D_i}\varphi( \nu_t^iu+ \nu_x^if(u))\,\mathrm{d}\ell \nonumber\\=&\int_{\Gamma}\varphi( \nu_t^iu+ \nu_x^if(u))\,\mathrm{d}\ell \nonumber\end{align}が成り立つ。ただし $\Gamma=\left\{(x,t)\in D\mid x=x(t) \right\}$ で、 $\nu^i=( \nu^i_t, \nu^i_x)$ は $D_i$ の外向き法線ベクトル。よって、 $u$ が弱解とすると\begin{align}0&=\int_D(\partial_t\varphi\cdot u+\partial_x\varphi\cdot f(u))\,\mathrm{d}x\mathrm{d}t \nonumber\\&=\left(\int_{D_l}+\int_{D_r} \right)(\partial_t\varphi\cdot u+\partial_x\varphi\cdot f(u))\,\mathrm{d}x\mathrm{d}t \nonumber\\&=\int_\Gamma\left(\varphi(\nu_t^lu_l+ \nu_x^lf_l)+\varphi(\nu_t^ru_r+ \nu_x^rf_r) \right)\,\mathrm{d}\ell \nonumber\\&=\int_\Gamma\left(\varphi(\nu_t^lu_l+ \nu_x^lf_l)-\varphi(\nu_t^lu_r+\nu_x^lf_r) \right)\,\mathrm{d}\ell \nonumber\\&=\int_\Gamma\varphi\left(\nu_t^l\left(u_l-u_r \right)+ \nu_x^l\left(f_l-f_r \right) \right)\,\mathrm{d}\ell \nonumber\end{align}が従います。 $\varphi$ は任意なので、変分学の基本補題より\begin{equation}\nu_t^l(u_l-u_r)+ \nu_x^l(f_l-f_r)=0\end{equation}となりますが、 $\dfrac{ \nu_t^l}{\nu_x^l}=-\dfrac{\mathrm{d}x}{\mathrm{d}t}$ なので\begin{equation}-\dfrac{\mathrm{d}x}{\mathrm{d}t}(u_l-u_r)+(f_l-f_r)=0\end{equation}となり、ランキン・ユゴニオ条件が満たされます。逆は変分学の基本補題の逆が自明なので上の議論を逆にたどっていけば成り立ちます。■

これでランキン・ユゴニオの正体がようやくわかりました。つまり、ランキン・ユゴニオとは、衝撃波の速度 $\dfrac{\mathrm{d}x}{\mathrm{d}t}$ と''保存''量の変化 $f_l-f_r$ の関係式のことだったんですね。定常の場合は前者がゼロで、保存量の変化がゼロということで、最初にやったような各種保存量の保存則が出てきたんですね。

渋滞もランキン・ユゴニオで説明できる！？

最後に、今出てきたランキン・ユゴニオ条件を用いてちょっとした応用をしてみたいと思います。題材は航空宇宙で最も有名な教授の一人、我らが西成活裕先生が研究している渋滞、とくに交通流のモデルを扱ってみましょう。設定としては

一車線のみで車の位置は $x$ で表せる。
位置 $x$ を時刻 $t$ に通過する車の数は、車の密度 $\rho(x,t)$ と速度 $v(x,t)$ を用いて $\rho v$ で与えられる。なので、 $\rho$ についての保存則として、次式が成り立つ。\begin{equation}\frac{\partial\rho}{\partial t}+\frac{\partial}{\partial x}(\rho v)=0\end{equation}。
車の数が少なければ、車は速く走る。
$v=v(\rho)$
車の数が増えると速度が減少する。すなわち $v$ は $\rho$ の減少関数。
ある密度 $\rho_{\max}$ 以上になると $v=0$

上記を満たすような $v$ にはいろいろなモデルが提案されていますが、今回は簡単な線形モデル\begin{equation}v=v_{\max}\left(1-\frac{\rho}{\rho_{\max}} \right)\end{equation}（ただし $v_{\max}$ は適当な正定数）を用いてみます。このとき $\displaystyle f(\rho)=\rho v_{\max}\left(1-\frac{\rho}{\rho_{\max}}\right)$ となります。

この交通流が渋滞したとき、つまり、ある時刻 $t=0$ で $x=0$ より前では $\rho=\rho_r=\rho_{\max}$ となり、それより後ろでは $\rho=\rho_l\lt\rho_{\max}$ となった状況を考えましょう。式で解の形を記述すると次のようになりますね。\begin{equation}\rho_0=\begin{cases}\rho_{\max}&(x\gt 0)\\ \rho_l&(x<0)\end{cases}\end{equation}

f:id:nobo0409mathinfo:20191201042051p:plain — 交通流のモデル。http://www.clawpack.org/riemann_book/html/Traffic_flow.htmlより引用

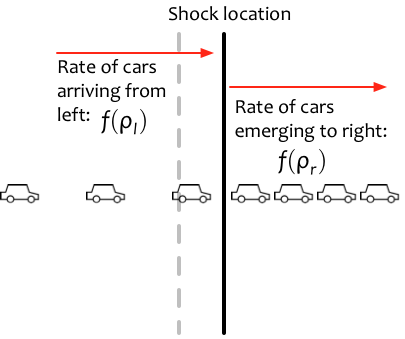
初期条件がこのように与えられた保存則が衝撃波解、弱解を持つ条件がランキン・ユゴニオ条件からわかるのでした。すなわち、衝撃波の速度、渋滞の境目が動く速度は\begin{equation}\frac{\mathrm{d} x}{\mathrm{d} t}=\frac{f(\rho_l)-f(\rho_r)}{\rho_l- \rho_{r}}=-\frac{ \rho_{l}v_{\max}}{\rho_{\max}}\lt0\end{equation}となります。

ここからわかるのは渋滞の境目は後ろに進んでいくということです。数式で言われても。。。という方も多いと思うので、次の動画で実際に実験してみた様子をご覧ください。

たしかに渋滞は後ろに伝わっていきます！これはちょっと感動しませんか？？？笑

まとめ

ここまで読んでいただいた方、ありがとうございました。多分読み飛ばしてここまで来た方もいらっしゃると思うので、この記事の内容をまとめておくと

まとめ圧縮性流体力学の入門として扱われるランキン・ユゴニオ関係式は、保存則という観点、そして、衝撃波を弱解で扱うという工夫により、一般に不連続面（衝撃波）の速度と"保存"量変化の関係を表し、その一般化によって渋滞現象の解析も可能となる。

って感じです。

できれば保存則の数値計算についてもお話ししたかったのですが、この記事を書いていたら12月になってしまったので今日はこの辺で。読んでいただきありがとうございました。

これ以降のアドベントカレンダーの記事はもっと面白いと思うので、お時間ある方は是非毎日見ていってくださいな。

それでは、素敵な12月をお過ごしください～～～

真空から。

今は航空学徒、春から数理情報学徒になるひとの備忘録やメモです。

ランキン・ユゴニオってそんなに大事？～圧縮性流体入門から保存則の偏微分方程式論、そして渋滞へ～

圧縮性流体力学超入門～Rankine-Hugoniot 関係式導出～

保存則、弱解の導入と保存則に対するランキン・ユゴニオ条件

渋滞もランキン・ユゴニオで説明できる！？

まとめ